publications

2024

1. MLST

   

   Large Language Models for Causal Hypothesis Generation in Science

   Kai-Hendrik Cohrs, Emiliano Diaz, Vasileios Sitokonstantinou, Gherardo Varando, and Gustau Camps-Valls

   Machine Learning: Science and Technology, Jan 2024

   Abs Bib HTML

   Towards the goal of understanding the causal structure underlying complex systems - such as the Earth, the climate, or the brain - integrating Large Language Models (LLMs) with data-driven and domain-expertise-driven approaches has the potential to become a game-changer, especially in data and expertise-limited scenarios. Debates persist around LLMs’ causal reasoning capacities. However, rather than engaging in philosophical debates, we propose integrating LLMs into a scientific framework for causal hypothesis generation alongside expert knowledge and data. Our goals include formalizing LLMs as probabilistic imperfect experts, developing adaptive methods for causal hypothesis generation, and establishing universal benchmarks for comprehensive comparisons. Specifically, we introduce a spectrum of integration methods for experts, LLMs, and data-driven approaches. We review existing approaches for causal hypothesis generation and classify them within this spectrum. As an example, our hybrid (LLM + data) causal discovery algorithm illustrates ways for deeper integration. Characterizing imperfect experts along dimensions such as 1) reliability, 2) consistency, 3) uncertainty, and 4) content vs. reasoning are emphasized for developing adaptable methods. Lastly, we stress the importance of model-agnostic benchmarks.

   @article{Kohrs_2025,
     doi = {10.1088/2632-2153/ada47f},
     url = {http://iopscience.iop.org/article/10.1088/2632-2153/ada47f},
     year = {2024},
     month = jan,
     publisher = {IOP Publishing},
     author = {Cohrs, Kai-Hendrik and Diaz, Emiliano and Sitokonstantinou, Vasileios and Varando, Gherardo and Camps-Valls, Gustau},
     title = {Large Language Models for Causal Hypothesis Generation in Science},
     journal = {Machine Learning: Science and Technology}
   }

2. App. Soft. Comp.

   

   Pairwise causal discovery with support measure machines

   Gherardo Varando, Salvador Catsis, Emiliano Diaz, and Gustau Camps-Valls

   Applied Soft Computing, Jan 2024

   Abs Bib HTML

   Bivariate causal discovery amounts to inferring the causal association between two random variables, usually from observational data. This task is the simplest and most fundamental causal discovery problem from which more complex discovery methods can be envisioned and developed. Classical bivariate causal discovery methods exploit a combination of specific sets of assumptions and data to obtain identifiability of the causal direction. Data-driven supervised approaches train machine learning models over large sets of causally-labeled bivariate datasets to learn the task of inferring the causal relationship from data. In this work, an ensemble algorithm based on support measure machines is proposed with the aim of combining the strength of different classical approaches (base methods) with data-driven decisions. In particular, support measure machine classifiers are trained to estimate the performance of each base method. Their decision functions are then used as data-dependent weights of a weighted voting scheme to estimate the causal direction in a bivariate causal discovery problem. This work demonstrates that the proposed algorithm, denoted as Causal Ensemble Measure Machine, performs equal to or better than state-of-the-art methods on a wide range of synthetic and real-world bivariate problems. Perhaps more importantly, this method enables a closer examination of the assumption dependence of existing algorithms on observational data.

   @article{VARANDO2024111030,
     title = {Pairwise causal discovery with support measure machines},
     url = {https://www.sciencedirect.com/science/article/pii/S1568494623010487},
     journal = {Applied Soft Computing},
     volume = {150},
     pages = {111030},
     year = {2024},
     issn = {1568-4946},
     doi = {https://doi.org/10.1016/j.asoc.2023.111030},
     author = {Varando, Gherardo and Catsis, Salvador and Diaz, Emiliano and Camps-Valls, Gustau},
     keywords = {Pairwise causal discovery, Kernel methods, Kernel mean embedding, Support vector machine, Ensemble methods}
   }

3. neurips workshop

   

   3D Cloud reconstruction through spatially aware masked autoencoders.

   Stella Girtsou Díaz Salas-Porras, Lilli Freischem, Joppe Massant, Kyriaki-Margarita Bintsi, Guiseppe Castiglione, and 4 more authors

   Jan 2024

   Bib HTML

   @misc{girtsou20243dCloud,
     title = {3D Cloud reconstruction through spatially aware masked autoencoders.},
     author = {andEmiliano Díaz Salas-Porras, Stella Girtsou and Freischem, Lilli and Massant, Joppe and Bintsi, Kyriaki-Margarita and Castiglione, Guiseppe and Jones, William and Eisinger, Michael and Johnson, Emmanuel and Jungbluth, Anna},
     url = {https://ml4physicalsciences.github.io/2024/files/NeurIPS_ML4PS_2024_255.pdf},
     year = {2024},
     eprint = {2501.02035},
     archiveprefix = {arXiv},
     primaryclass = {cs.CV}
   }

4. Arxiv

   

   Recovering Latent Confounders from High-dimensional Proxy Variables

   Nathan Mankovich, Homer Durand, Emiliano Diaz, Gherardo Varando, and Gustau Camps-Valls

   Jan 2024

   Bib HTML

   @misc{mankovich2024recovering,
     title = {Recovering Latent Confounders from High-dimensional Proxy Variables},
     author = {Mankovich, Nathan and Durand, Homer and Diaz, Emiliano and Varando, Gherardo and Camps-Valls, Gustau},
     url = {https://arxiv.org/abs/2403.14228},
     year = {2024},
     eprint = {2403.14228},
     archiveprefix = {arXiv},
     primaryclass = {stat.ML}
   }

5. Arxiv

   

   Causal machine learning for sustainable agroecosystems

   Vasileios Sitokonstantinou, Emiliano Díaz Salas Porras, Jordi Cerdà Bautista, Maria Piles, Ioannis Athanasiadis, and 6 more authors

   Jan 2024

   Bib HTML

   @misc{sitokonstantinou2024causalml,
     title = {Causal machine learning for sustainable agroecosystems},
     author = {Sitokonstantinou, Vasileios and Porras, Emiliano Díaz Salas and Bautista, Jordi Cerdà and Piles, Maria and Athanasiadis, Ioannis and Kerner, Hannah and Martini, Giulia and Sweet, Lily-belle and Tsoumas, Ilias and Zscheischler, Jakob and Camps-Valls, Gustau},
     url = {https://arxiv.org/abs/2408.13155},
     year = {2024},
     eprint = {2408.13155},
     archiveprefix = {arXiv},
     primaryclass = {cs.LG}
   }

2023

1. Physics Reports

   

   Discovering causal relations and equations from data

   Gustau Camps-Valls, Andreas Gerhardus, Urmi Ninad, Gherardo Varando, Georg Martius, and 5 more authors

   Physics Reports, Jan 2023

   Discovering causal relations and equations from data

   Abs Bib HTML

   

   Physics is a field of science that has traditionally used the scientific method to answer questions about why natural phenomena occur and to make testable models that explain the phenomena. Discovering equations, laws, and principles that are invariant, robust, and causal has been fundamental in physical sciences throughout the centuries. Discoveries emerge from observing the world and, when possible, performing interventions on the system under study. With the advent of big data and data-driven methods, the fields of causal and equation discovery have developed and accelerated progress in computer science, physics, statistics, philosophy, and many applied fields. This paper reviews the concepts, methods, and relevant works on causal and equation discovery in the broad field of physics and outlines the most important challenges and promising future lines of research. We also provide a taxonomy for data-driven causal and equation discovery, point out connections, and showcase comprehensive case studies in Earth and climate sciences, fluid dynamics and mechanics, and the neurosciences. This review demonstrates that discovering fundamental laws and causal relations by observing natural phenomena is revolutionised with the efficient exploitation of observational data and simulations, modern machine learning algorithms and the combination with domain knowledge. Exciting times are ahead with many challenges and opportunities to improve our understanding of complex systems.

   @article{CAMPSVALLS20231,
     url = {https://www.sciencedirect.com/science/article/pii/S0370157323003411},
     title = {Discovering causal relations and equations from data},
     journal = {Physics Reports},
     volume = {1044},
     pages = {1-68},
     year = {2023},
     dimensions = {true},
     google_scholar_id = {qyhmnyLat1gC},
     note = {Discovering causal relations and equations from data},
     issn = {0370-1573},
     doi = {https://doi.org/10.1016/j.physrep.2023.10.005},
     author = {Camps-Valls, Gustau and Gerhardus, Andreas and Ninad, Urmi and Varando, Gherardo and Martius, Georg and Balaguer-Ballester, Emili and Vinuesa, Ricardo and Diaz, Emiliano and Zanna, Laure and Runge, Jakob},
     keywords = {Causal inference, Causal discovery, Complex systems, Nonlinear dynamics, Equation discovery, Knowledge discovery, Understanding, Artificial intelligence, Neuroscience, Climate science}
   }

2. MLST

   

   Learning latent functions for causal discovery

   Emiliano Díaz, Gherardo Varando, J Emmanuel Johnson, and Gustau Camps-Valls

   Machine Learning: Science and Technology, Jul 2023

   Abs Bib HTML PDF

   Causal discovery from observational data offers unique opportunities in many scientific disciplines: reconstructing causal drivers, testing causal hypotheses, and comparing and evaluating models for optimizing targeted interventions. Recent causal discovery methods focused on estimating the latent space of the data to get around a lack of causal sufficiency or additivity constraints. However, estimating the latent space significantly increases model complexity, compromising causal identifiability and making it hard to compare models that correspond to different causal hypotheses. We propose a kernel, non-parametric latent-space modelling approach and deal with the difficulty of comparing causal directions by measuring and controlling for the level of causal assumption fulfilment. We introduce a latent noise causal inference framework to estimate latent factors associated with the hypothesized causal direction by optimizing a loss function with kernel independence criteria. We extend the framework to work with time series using an additional time-dependent kernel regularizer. We discuss the additivity assumption and model complexity and give empirical evidence of performance in a wide range of synthetic and real causal discovery problems.

   @article{Díaz_2023,
     doi = {10.1088/2632-2153/ace151},
     url = {https://dx.doi.org/10.1088/2632-2153/ace151},
     year = {2023},
     month = jul,
     publisher = {IOP Publishing},
     volume = {4},
     number = {3},
     pages = {035004},
     author = {Díaz, Emiliano and Varando, Gherardo and Johnson, J Emmanuel and Camps-Valls, Gustau},
     title = {Learning latent functions for causal discovery},
     journal = {Machine Learning: Science and Technology}
   }

3. Arxiv

   

   Large Language Models for Constrained-Based Causal Discovery

   Kai-Hendrik Cohrs, Emiliano Diaz, Vasileios Sitokonstantinou, Gherardo Varando, and Gustau Camps-Valls

   In AAAI 2024 Workshop on ”Are Large Language Models Simply Causal Parrots?” , Jul 2023

   Bib HTML

   @inproceedings{cohrs2023large,
     title = {Large Language Models for Constrained-Based Causal Discovery},
     author = {Cohrs, Kai-Hendrik and Diaz, Emiliano and Sitokonstantinou, Vasileios and Varando, Gherardo and Camps-Valls, Gustau},
     url = {https://openreview.net/forum?id=NEAoZRWHPN},
     booktitle = {AAAI 2024 Workshop on ''Are Large Language Models Simply Causal Parrots?''},
     year = {2023}
   }

2022

1. Env. research letters

   

   Physics-aware nonparametric regression models for Earth data analysis

   Jordi Cortés-Andrés, Gustau Camps-Valls, Sebastian Sippel, Enikő Székely, Dino Sejdinovic, and 5 more authors

   Environmental Research Letters, May 2022

   Abs Bib HTML

   Process understanding and modeling is at the core of scientific reasoning. Principled parametric and mechanistic modeling dominated science and engineering until the recent emergence of machine learning (ML). Despite great success in many areas, ML algorithms in the Earth and climate sciences, and more broadly in physical sciences, are not explicitly designed to be physically-consistent and may, therefore, violate the most basic laws of physics. In this work, motivated by the field of algorithmic fairness, we reconcile data-driven ML with physics modeling by illustrating a nonparametric and nonlinear physics-aware regression method. By incorporating a dependence-based regularizer, the method leads to models that are consistent with domain knowledge, as reflected by either simulations from physical models or ancillary data. The idea can conversely encourage independence of model predictions with other variables that are known to be uncertain either in their representation or magnitude. The method is computationally efficient and comes with a closed-form analytic solution. Through a consistency-vs-accuracy path diagram, one can assess the consistency between data-driven models and physical models. We demonstrate in three examples on simulations and measurement data in Earth and climate studies that the proposed ML framework allows us to trade-off physical consistency and accuracy.

   @article{Cortés-Andrés_2022,
     doi = {10.1088/1748-9326/ac6762},
     url = {https://dx.doi.org/10.1088/1748-9326/ac6762},
     year = {2022},
     month = may,
     publisher = {IOP Publishing},
     volume = {17},
     number = {5},
     pages = {054034},
     author = {Cortés-Andrés, Jordi and Camps-Valls, Gustau and Sippel, Sebastian and Székely, Enikő and Sejdinovic, Dino and Diaz, Emiliano and Pérez-Suay, Adrián and Li, Zhu and Mahecha, Miguel and Reichstein, Markus},
     title = {Physics-aware nonparametric regression models for Earth data analysis},
     journal = {Environmental Research Letters}
   }

2. Scientific Reports

   

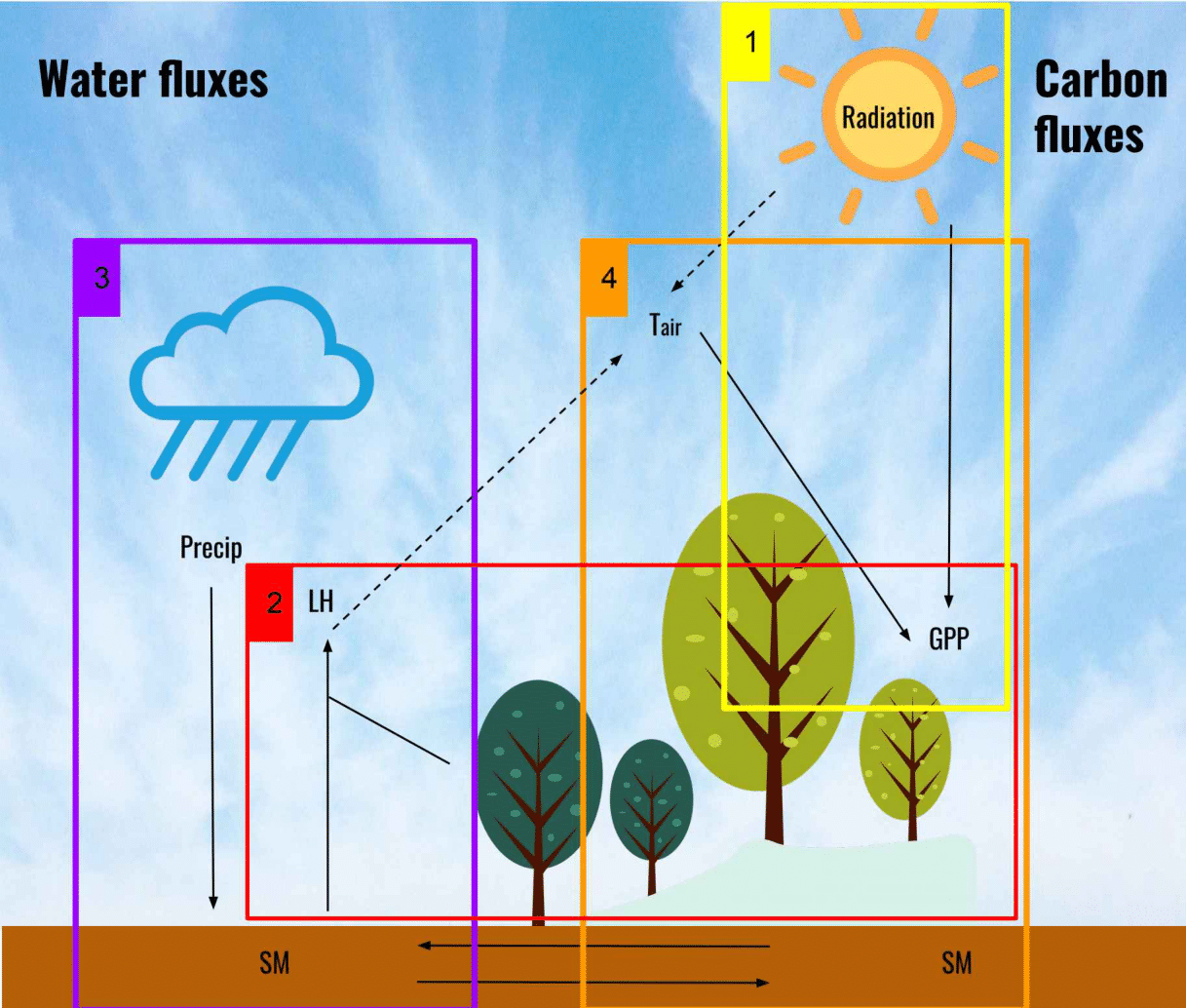   Inferring causal relations from observational long-term carbon and water fluxes records

   Emiliano Díaz, Jose Adsuara, Alvaro Moreno, Maria Piles, and Gustau Camps-Valls

   Scientific Reports, Jan 2022

   Abs Bib HTML

   Land, atmosphere and climate interact constantly and at different spatial and temporal scales. In this paper we rely on causal discovery methods to infer spatial patterns of causal relations between several key variables of the carbon and water cycles: gross primary productivity, latent heat energy flux for evaporation, surface air temperature, precipitation, soil moisture and radiation. We introduce a methodology based on the convergent cross-mapping (CCM) technique. Despite its good performance in general, CCM is sensitive to (even moderate) noise levels and hyper-parameter selection. We present a robust CCM (RCCM) that relies on temporal bootstrapping decision scores and the derivation of more stringent cross-map skill scores. The RCCM method is combined with the information-geometric causal inference (IGCI) method to address the problem of strong and instantaneous variable coupling, another important and long-standing issue of CCM. The proposed methodology allows to derive spatially explicit global maps of causal relations between the involved variables and retrieve the underlying complexity of the interactions. Results are generally consistent with reported patterns and process understanding, and constitute a new way to quantify and understand carbon and water fluxes interactions

   @article{rccm,
     author = {Díaz, Emiliano and Adsuara, Jose and Moreno, Alvaro and Piles, Maria and Camps-Valls, Gustau},
     url = {https://www.nature.com/articles/s41598-022-05377-7},
     year = {2022},
     month = jan,
     pages = {1610},
     title = {Inferring causal relations from observational long-term carbon and water fluxes records},
     volume = {12},
     journal = {Scientific Reports},
     doi = {10.1038/s41598-022-05377-7}
   }

3. neurips workshop

   

   Identifying the Causes of Pyrocumulonimbus (PyroCb)

   Emiliano Díaz Salas-Porras, Kenza Tazi, Ashwin Braude, Daniel Okoh, Kara D. Lamb, and 3 more authors

   Jan 2022

   Bib HTML

   @misc{salasporras2022identifying,
     title = {Identifying the Causes of Pyrocumulonimbus (PyroCb)},
     author = {Salas-Porras, Emiliano Díaz and Tazi, Kenza and Braude, Ashwin and Okoh, Daniel and Lamb, Kara D. and Watson-Parris, Duncan and Harder, Paula and Meinert, Nis},
     url = {https://openreview.net/forum?id=rM6HO4h1MI},
     year = {2022},
     eprint = {2211.08883},
     archiveprefix = {arXiv},
     primaryclass = {stat.ML}
   }

4. Neurips workshop

   

   Pyrocast: a Machine Learning Pipeline to Forecast Pyrocumulonimbus (PyroCb) Clouds

   Kenza Tazi, Emiliano Díaz Salas-Porras, Ashwin Braude, Daniel Okoh, Kara D. Lamb, and 3 more authors

   . More Information can be found here , Jan 2022

   Bib HTML Video

   @misc{tazi2022pyrocast,
     title = {Pyrocast: a Machine Learning Pipeline to Forecast Pyrocumulonimbus (PyroCb) Clouds},
     author = {Tazi, Kenza and Salas-Porras, Emiliano Díaz and Braude, Ashwin and Okoh, Daniel and Lamb, Kara D. and Watson-Parris, Duncan and Harder, Paula and Meinert, Nis},
     url = {https://openreview.net/forum?id=00zFXUmhNUl},
     html2 = {https://openreview.net/forum?id=00zFXUmhNUl},
     year = {2022},
     eprint = {2211.13052},
     archiveprefix = {arXiv},
     primaryclass = {physics.ao-ph}
   }